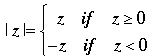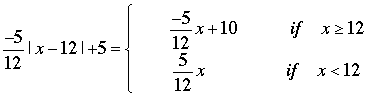| |||
| Math Central | Quandaries & Queries |
|
Question from Sandi, a student: This question has been haunting my dreams at night. It states the cross section of the roof of a house is modelled by the function y= -5\12|x-12|+5, where y>0 or y. Now I'm suppose to graph the function. b) Find the slope, height, length of sides, and base of the isosceles triangle. c)Explain what transformation must be applied to the graph of y=|x| to obtain the graph of y= -5\12|x-12|+5, where y>0 or y=0. 1st I put the equation into my calculator and graphed it. I got 10 for the height. We have had 2 sub teachers this past week. The first one told me the height should be 12 the other one told me 5. So I'm really confused. If I use my 10 units as height and the Pythagorean Theorem I get my sides to be 26 units the base 48 and my slope I calc to be 5/12. Both teachers are pretty sure I'm wrong and they are right but we all have different answers. Please help put this problem to rest so I can rest soundly at night. Thank you for your time. |
Hi Sandi,
Let's graph it without the calculator, using the definition of absolute value.
Hence if |x - 12| ≥ 0 then y= -5\12|x - 12| + 5 = y= -5\12 (x - 12) + 5 = -5/12 x + 5 + 5 = -5/12x + 10.
If |x - 12| < 0 then y= -5\12|x - 12| + 5 = y= -5\12 [-(x - 12)] + 5 = 5/12 x - 5 + 5 = 5/12x.
But |x - 12| ≥ 0 if x ≥ 12 and |x - 12| < 0 if x < 12 so
Thus for x < 12 the graph is a straight line with slope 5/12 and passing through the origin. When x is close to 12 the value of the function is close to 5.
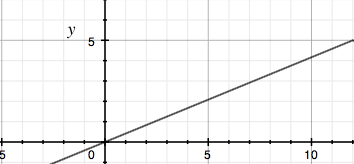
When x ≥ 12 the slope changes to -5/12 and when x = 12 the value of the function is 5.
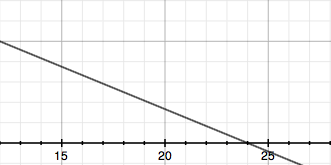
Putting the two parts together gives
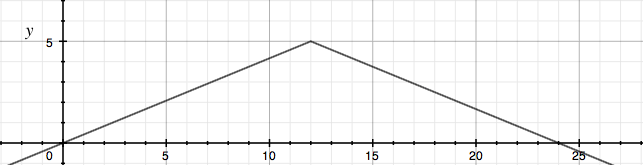
Can you finish the problem now? Write back if you need more help,
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.