Hi Sarah,

The volume of a pyramid is (1/3) × (area of the base) × height, so you first need to know the area of the hexagonal base and the hexagonal top of the frusta. If the hexagon is regular you can use the technique that Stephen explained in a response to Scott. If the hexagon is not regular then the technique to find the area depends on what you know about the hexagon. See RD's response to a question from Vicki.

The volume of the frustum is then the difference of the volumes of two hexagonal pyramids one with height H units and the other with height h units as in the diagram.

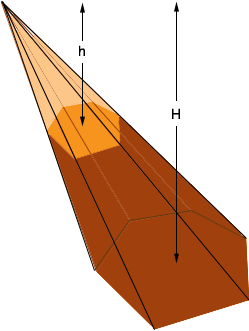
Is the pyramid is a right pyramid, that does the line from the apex to the centre of the base form a right angle with the base?

Penny