Modelling an underpass - Math Central

HOME

Math Central

Quandaries & Queries

Question from Sue, a student:

An engineer at the Ministry of Transport is creating the plans for a new road. This road
will cross the path of a busy railway track so it will be necessary to built an underpass for this road.
This underpass will be in the shape of a parabolic arch.

The specifications include:
-the road must be at least 10 m wide and it must have shoulders at least 2 m wide on either
side of the road.
-there must be a clearance of 3 m over all areas of the road.

What quadratic equation could you use to model this bridge.

Hi Sue,

I drew a diagram of what you described with the measurements in metres.

arch

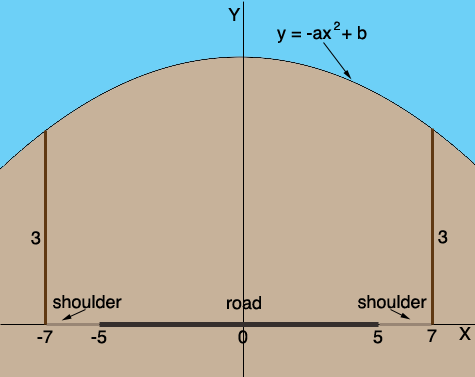
I introduced an X and Y axis with the road on the X-axis and the Y-axis passing through the vertex of the parabola. Since this is a parabola that opens downward and the vertex is above the X-axis I can write its equation y = -ax² + b where a and b are positive. Do you see why a and b must be positive?

Since there must be at least a 3 m clearance over all areas of the road when x = 7, y must be at least 3. In order to not make the bridge higher than it needs to be let y = 3 when x = 7. Thus

3 = -a7² + b.

Solve this equation for b and substitute into y = -ax² + b. This will give you a model with a still to be determined from other considerations. For example how high is the bridge at its highest point? What is a if this height is 5 metres? What if it's only 4 metres?

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.