Hi Susan,

Cute project!

Here is a sketch of the cone shaped top.

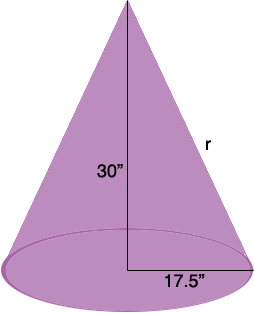
You have a right triangle with legs of length 17.5" and 30" and hypotenuse of length r inches so Pythagoras theorem says that

17.5² + 30² = r²

or

r = 34.7 inches.

If you took the material from the cone in the diagram and cut it along one of the seams it will then lie flat in the shape of a sector of a circle as in the diagram below.

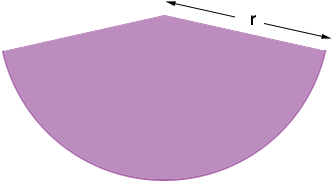
The circumference of the hula hoop is π × diameter = π × 35 = 109.0 inches which is the length of the arc in the sector above. This is a sector of a circle with radius 34.7 inches or diameter 69.4 inches so the circumference of this circle is π × diameter = π × 69.4 = 218.0 inches. Thus the arc length is half the circumference and hence the sector is a semicircle.

Hence if you cut a semicircle of radius 34.7 inches which is about 34 3/4 inches it will form the cone you need. Unfortunately this leaves no material for a seam. If your material is 36 inches wide I would cut a piece like this

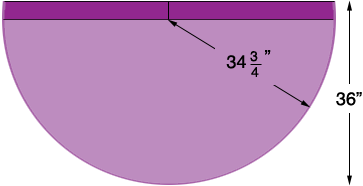
leaving you an inch and a quarter for seams.

If you complete this project send us a photo so we can post it.

Penny