| |||
| Math Central | Quandaries & Queries |
|
Question from Terry, a student: The vertex of a right circular cone and the circular edge of its base lie on the surface of a sphere with a radius of 2m. Find the dimensions of the cone of maximum volume that can be inscribed in the sphere. |
Terry,
In my diagram C is the center of the sphere, R is its radius so in your situation R = 2 m, h is the height of the cone and r is the radius of the base of the cone. All the dimensions are in meters.
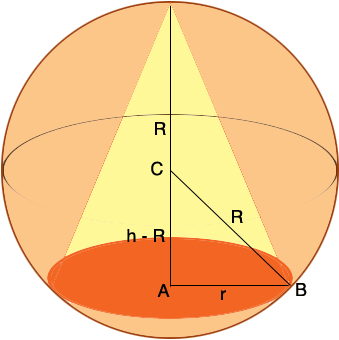
The volume of a cone is V = 1/3 π r2 h and this is what you want to maximize. The task as usual with this type of problem is to write V a a function of one variable alone so you need an expression relating r and h so that you can eliminate one of them. I would use the right triangle ABC. Pythagoras theorem will give you an expression that allows you to substitute for r2 in the expression for the volume and leave you with an expression for h alone since you know the value of R.
Apply the calculus you know to maximize V.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.