| |||
| Math Central | Quandaries & Queries |
|
Question from Wayne: Given the length & radius of an arc, is there a formula that will accurately calculate the chord length? |
Wayne,
I would do it in 2 steps.
Step 1:
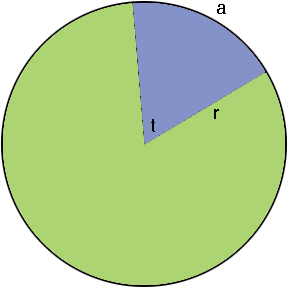
Find the measure of the angle t in the diagram.
The length a of the arc is a fraction of the length of the circumference which is 2 π r. In fact the fraction is
.
The angle t is a fraction of the central angle of the circle which is 360 degrees. It's the same fraction. Thus
t = 360 ×
degrees.
Step2:
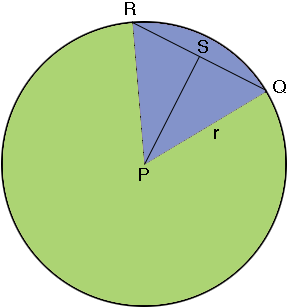
Find the length c of the chord RQ in the diagram
S is the midpoint of RQ so |SQ| = c/2 and the measure of the angle SPQ is t/2. Also QSP is a right angle so sin(t/2)= |SQ|/r. Hence |SQ| = r × sin(t/2) and thus
c = 2 × r × sin(t/2).
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.