| |||
| Math Central | Quandaries & Queries |
|
Question from freitas, a student: the top plane of the truncated octagonal right prism is 45 degree with respect to horizontal. find the volume |
Hi Freitas,
First to understand the problem let's look a right octagonal prism:
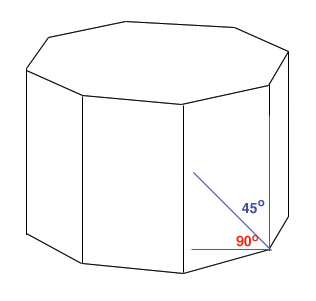 |
A right prism means that the base and the height create a 90o angle. If the prism is truncated at 45o with the horizontal that means that the prism is divided in half, in other words we need to find half of the volume of a right octagonal prism. Since Volume = Area × height we need to find half of that volume. So for the truncated volume: Volume = 1/2 Area × height |
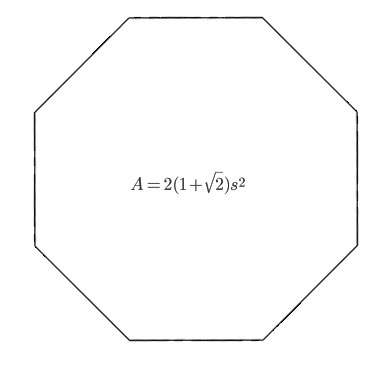 |
A right octagonal prism implies that is a regular polygon where all sides are equal. In this case, s is the length of one side of the octagon. |
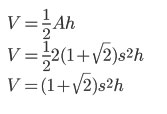 |
Combining the two formulae together, we get the volume on the right |
Hope this helps,
Janice
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.