Hi Adori,

You know that $\tan \theta = \frac{\sin \theta}{\cos \theta}$. Suppose $\theta$ moves around the circle from $0$ to $2 \pi$. For $\theta$ between $0$ and $\frac{\pi}{4}, \cos \theta > \sin \theta$ so $\tan \theta < 1. \tan \frac{\pi}{4} = 1$ and then for some $\theta_1$ slightly larger than $\frac{\pi}{4}, \tan \theta_1 = 1.192.$ Your calculator will give a much better approximation for $\theta_1$ but it will be slightly larger than $\frac{\pi}{4} = 0.7853$ radians.As $\theta$ continues to increase to $\frac{\pi}{2}, \cos \theta$ decreases to $0$ and $\sin \theta$ increases to $1$ so $\tan \theta \neq 1.192$ in this interval.

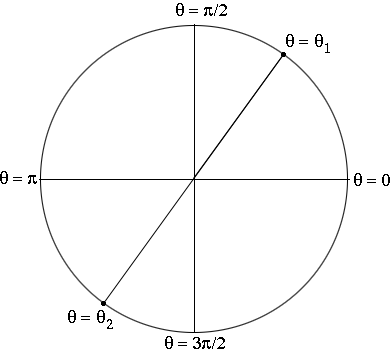
For $\frac{\pi}{2} < \theta < \pi, \cos \theta < 0$ and $\sin \theta > 0$ so $\tan \theta$ is negative. Likewise for $\frac{3 \pi}{2} < \theta < 2 \pi, \tan \theta$ is also negative. But for some $\theta_2$ between $\pi$ and $\frac{3 \pi}{2},$ as in the diagram, $\tan \theta_2 = 1.192.$ What is the radian measure of $\theta_2?$

Harley