Hi,

I would use a tree diagram to approach this problem. Assume that A goes first.

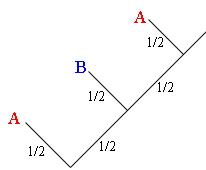
At the first branch point in my tree the coin is tossed by A. If she tosses a head take the left branch and she wins.If she tosses a tail take the right branch and then B tosses the coin. If she tosses a head take the left branch and B wins. If she tosses a tail take the right branch and A tosses the coin again.

At each branch point the probability of tossing a head is $\frac12$ so the probability that A wins on the first toss ia $\frac12.$ For A to win on her second toss she must lose on her first toss, B must lose on her first toss and A must win on her second toss. Each of these results has a probability so the probability that A wins on her second toss is $\frac12 \times \frac12 \times \frac12.$Hence the probability that A wins in a 3 toss game is $\frac12 + \frac12 \times \frac12 \times \frac12.$

What is the probability that she wins in a 5 toss game given that she tosses first?

Penny