Hi Bill,

The volume is the area of the cross-section times the length of 200 feet. From your description I see the cross-section as

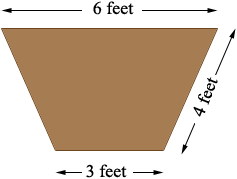
If this is correct then in the diagram below |AC|, the distance from A to C is (6 - 3)/2 = 1.5 feet.

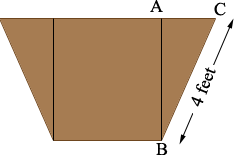
Triangle ABC is a right triangle and hence from the Theorem of Pythagoras |AB|² = 4² - 1.5² = 13.75 and thus |AB| = √13.75 = 3.7 feet.

The shape of the cross-section is a trapezoid and the area of a trapezoid is

(the average of the lengths of the parallel sides) times the distance between the parallel sides.

In your case this gives

1/2 × (6 + 3) × 3.7 = 16.7 square feet.

Hence the volume of dirt to be removed is

16.7 × 200 = 3337.3 cubic feet.

A cubic yard is 3 feet by 3 feet by 3 feet so its volume is 3 × 3 × 3 = 27 cubic feet and thus the volume of dirt to be removed is

3337.3/27 = 123.6 cubic yards.

Penny