Hi Bill. We can work out a formula.

You have the top diameter and the bottom diameter. If you divide those in two, it will simplify things. Call the top radius $T$ and the bottom radius $B$. You will also need to measure the full slant height. Let's call that $S$. That completes the measurements for the container. You also need to measure the slant height $s$ of the liquid. The task now is to write the volume of liquid in terms of $T, B, S \mbox{ and } s.$

The shape of the liquid is called a truncated cone and the volume of a truncated cone is given by

\[V = \frac13 \pi \, h (R^2 + rR + r^2)\]

where $R \mbox{ and }r$ are the radii of the top and bottom and $h$ is the vertical height.

The radius of the bottom of the liquid is the same as the radius of the bottom of the container: $B,$ but the radius of the top surface of the liquid has to be calculated. We need to know the horizontal distance between the bottom of the tank and the liquid surface. We can find the radius of the top of the liquid using similar triangles. The ratios of corresponding sides of similar triangles are equal.

I'll assume the container is wider at the top than the bottom (if not, use $B-T$ rather than $T-B$ in these calculations). Here is a diagram.

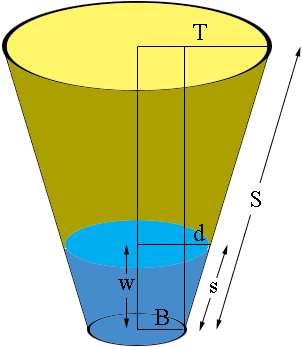
Look the right-angled triangle formed with a corner at the bottom rim of the container, a hypotenuse going up $S$ units, and a horizontal leg at the top. That horizontal leg has length the difference in the radii of the bottom and the top ($T-B$). That's a similar triangle to the one formed with the liquid.

The triangle formed at the container's side is similar to the triangle in the liquid. That means that

$\large \frac s S = \frac d {T-B}$

where $d$ is shown in the diagram. Hence $d = \frac sS (T - B).$

So we can find $d$ which is the horizontal part of the liquid's triangle. If $L$ is the radius of the top of the liquid and we know that the radius of the bottom of the liquid is $B$ then, assuming the tapering of the container is outwards (the top is larger than the base), this means $L = B + d$. Thus

\[L = B + \frac sS (T - B).\]

All that remains is to find the depth of liquid in the tank, labeled $w$ in the diagram. Looking at the diagram again, the triangle with sides of length $w, d \mbox{ and } s$ is a right triangle so using Pythagoras' theorem $s^2 = w^2 + d^2.$ Substituting $d = \frac sS (T - B).$ and solving for $w$ gives

\[w = \frac sS \sqrt{S^2 - (T - B)^2}\]

Now we are finished. Using the formula for the volume of a truncated cone

\[V = \frac13 \pi \, h (R^2 + rR + r^2)\]

and substituting $h, R \mbox{ and }r$ for the the appropriate values for the liquid we get

\[V = \frac13 \pi \, \frac sS \sqrt{S^2 - (T - B)^2} \, (L^2 + LB + B^2)\]

where

\[L = B + \frac sS (T - B).\]

And we've completed the problem!

Cheers,
Stephen La Rocque and Penny Nom