Daima,

Suppose you have a convex pentagon $ABCDE$ as in the diagram below. Stand at $A,$ facing toward $B$ and start to walk around the polygon.

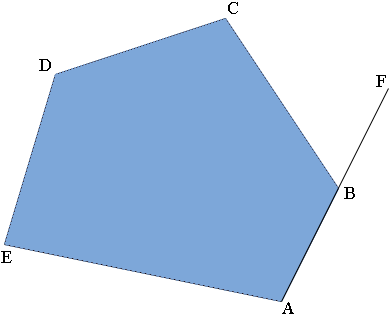
When you reach $B$ you need to turn through the angle $FBC$ to walk towards $C.$ The angle $FBC$ is called the external angle at $B$ and the angle $ABC$ is the interior angle at $B.$ Continue around the pentagon until you are back at $A$ facing $B.$ At each vertex you have turned through the external angle and now you are back where you started having made one complete revolution. Thus the sum of the external angles is 360 degrees. (Notice that I didn't use the fact that this is a pentagon. What I showed is that the sum of the external angles of a convex polygon is 360 degrees.)

But you wanted the interior angles. Each internal angle measures 180^o minus the the exterior angle at this vertex. Thus the sum of the measures of the interior angles is

(180 - exterior angle at $A$) + (180 - exterior angel at $B$) + ... + (180 - exterior angel at $E$)
= $5 \times 180$ - the sum of the exterior angles
= $5 \times 180 - 360 = 540 \mbox{ degrees.}$

I hope this helps,
Penny