Hi,

To say $\large \frac10$ is infinity is just a shorthand way to say that the fraction $\large \frac1x$ is unbounded as $x$ gets close to zero. Using the language of calculus this is

\[ \lim_{x \rightarrow 0^+} \frac1x = \infty \]

The plus sign superscript on zero means that I am restricting $x$ to be to the right of zero.

Look at the graph of $y = \large \frac1x.$

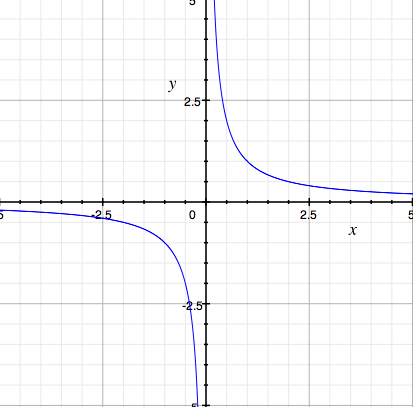
I would say "$\large \frac1x$ goes to infinity as $x$ goes to zero." Some textbooks or teachers may say "$\large \frac10 = \infty$".

So what about $\large \frac20?$ Look at the graphs of $\large \frac1x$ (in blue) and $\large \frac2x$ (in red) on the same plot.

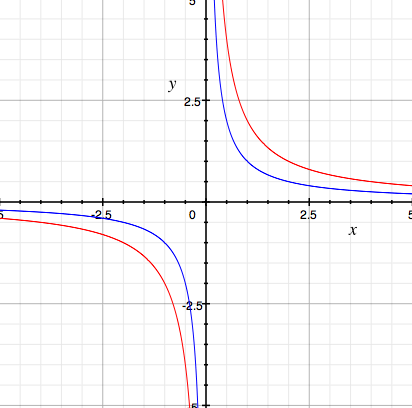
Again I would say "$\large \frac2x$ goes to infinity as $x$ goes to zero" or more precisely

\[ \lim_{x \rightarrow 0^+} \frac2x = \infty \]

If you are looking for a difference you might say "$\large \frac2x$ goes to $\infty$ twice as fast as $\large \frac1x.$" By this statement I mean that for any positive value of $x, \large \frac2x$ is twice as large as $\large \frac1x.$

I hope this helps,
Harley