Flipping a cone over - Math Central

HOME

Math Central

Quandaries & Queries

Question from Fionna, a student:

The height of your cone is "x".
Holding the cone so that the vertex is at the bottom, fill it half full with water. The depth of the water is "1/2x".
Put a lid over the top, and flip it over.
What is the new depth of the water, now that the cone is flipped?

Fionna,

Suppose the radius of the base of the cone is $r$ and the radius of the surface of the water is $w.$

cone

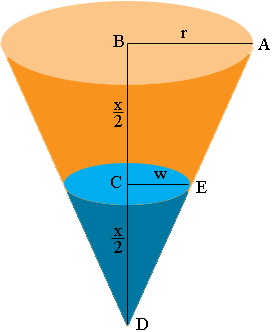
Triangles ABD and ECD are similar. Use this fact to find $w$ in terms of $r.$ Write the volume of the air space in the cone above the water as the volume of the cone minus the volume of the water. Simplify.

Now turn the cone over.

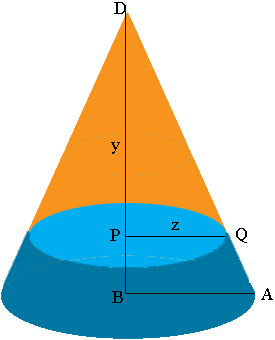
flipped

The air space is now a cone of height $y$ and base radius $z.$ Use similar triangles again to find a relationship between $y$ and $z.$ Write the volume of the cone shaped air space and use the relationship between $y$ and $z$ to eliminate $z$ from this expression. Set this volume equal to the volume of the air space you found in the previous paragraph and solve for $y.$

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.