| |||
| Math Central | Quandaries & Queries |
|
Question from Gary: I I was reading about how the number of points on a line is equivalent to that of a surface. This was done by taking any point on a line then taking alternating digits and making them as points on an x and y axis therefore points on a surface.The problem is as i see it if you just take a line then hold it over a surface you have just put the points on the line in a one to one correspondence with the points directly under it on the surface.Now you have all the rest of the surface which cannot be mapped onto the line since it is already used up.What am i missing? |
These things can be confusing but nevertheless correct. Let me illustrate with a simpler example. Consider the interval, or if you prefer, line segment (0,1). The number of points in this interval is the same as the number of points on the real line. One might say that if you were to hold this up over the real line that you have just put the points on this interval "in a one-to-one correspondence with the points directly under it" on the real line and there's all the rest of the real line not mapped; a problem. But look at this from a different perspective.
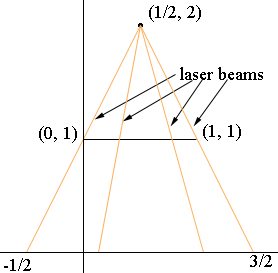
Suppose you are in the plane at the point (1/2, 2) and the interval (0,1) is suspended above the real line from the point (0,1) to the point (1,1). Shine a finely tuned laser beam from your position, across this suspended interval, and note where the beam passes through it and hits the real line. It will hit every point in the interval (-1/2, 3/2). Thus you have a one-to-one mapping of the interval (0,1) onto something twice as long! By varying your location you can extend this mapping to as much, or as little, of the whole real line as you please.
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.