A circle in a square in a circle in a square

HOME

Math Central

Quandaries & Queries

Question from George, a parent:

A circle within a square which is inside a larger circle which is also within a square. (a circle in a square inside a circle in a square)
Equation of the smaller circle is: x ^ 2 x y ^ 2 = 25.
What are the dimensions of the larger square?
Been 40 years, trying to help my son.

Hi George,

I think the equation of the smaller circle is $x^2 + y^2 = 25.$

A circle with centre at the origin and radius $r$ has equation $x^2 + y^2 = r^2$ and thus the smaller circle has radius 5 units. Here is my diagram. $C$ is the origin.

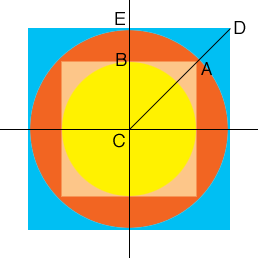
squares and circles

Triangle $ABC$ is a right triangle and $|AB| = |BC| = 5.$ Use Pythagoras' theorem to find the length of $CA.$ This is the radius of the larger circle.

Can you complete the problem now?

Rather than asking for the dimensions of the larger square I would have asked for the length of its diagonal. Can you find the length of the diagonal?

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.