Hi Gevork,

The area of a parallelogram is the base times the height. In my diagram below the height $h$ is related to the side of length 8 and the angle $\theta$ in radians by $\sin \theta = \frac{h}{8}.$

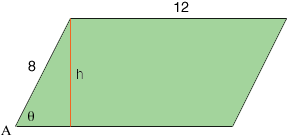
Solving this expression for $h$ and substituting into the area expression for the area gives

\[A(t) = 72 \sin \theta(t).\]

I have written the area $A$ and the angle $\theta$ as functions of time $t$ in minutes as they are both changing with respect to time. You can now differentiate both sides with respect to $t$ to find $\large \frac{dA}{dt}$ as a function of $\theta$ and $\large \frac{d\theta}{dt.}$

The remaining challenge is that $\theta$ is in radians and $\large \frac{d\theta}{dt}$ is in radians per minute and you have an angle of 30 degrees which is changing at -2 degrees per minute. To evaluate $\large \frac{dA}{dt}$ at the correct time you will need to convert radians to degrees using the fact that $\pi \mbox{ radians } = 180 \mbox{ degrees }.$

I hope this helps,
Penny