Guy,

Suppose the radius of the base is $r$ units and the lamp is to have $n$ sides. In the diagram below $AB$ is one of the sides of the trapezoid and the measure of the angle $BAC$ is $\large \frac{360}{n}$ degrees.

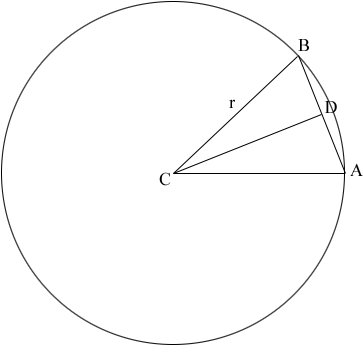
$D$ is the midpoint of $AB$ and hence the measure of the angle $BCD$ is $\large \frac{180}{n}$ degrees. Triangle $BCD$ is a right triangle and hence $\large \frac{|DB|}{r} = cos\left(\frac{180}{n}\right)$ or $|DB| = r cos\left(\frac{180}{n}\right).$ This if $|AB|,$ the length of $AB$ is $L$ then

\[L = 2\;r\;cos\left(\frac{180}{n}\right).\]

Finally perform the same calculation with $r$ the radius of the top of the lamp.

I hope this helps,
Harley

Guy wrote back with a note that contained

In your diagram, the line AB is a secant, bisecting the circle at 2 points. In my application, the line AB is a tangent intersecting the circle at point D. Therefore r isn't CB but CD. (r is one of the legs of the right triangle, not the hypotenuse.)

Guy,

We did have a miscommunication. In my diagram below, which is the base of a lamp with 5 sides, I took "diameter" to mean the diameter of the red circle where you meant the diameter of the blue circle.

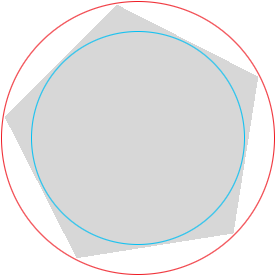
Suppose the diameter of this circle is $d$ then in my first diagram $|CD| = d/2.$ Then $\frac{|DB|}{|CD|} = tan\left(\frac{180}{n}\right)$ and hence

\[L = d\;tan\left(\frac{180}{n}\right).\]

Harley