Hanniel,

In my diagram $A$ is the centre of the black circle, $B$ is the centre of the red circle and $C$ is the centre of the blue circles.

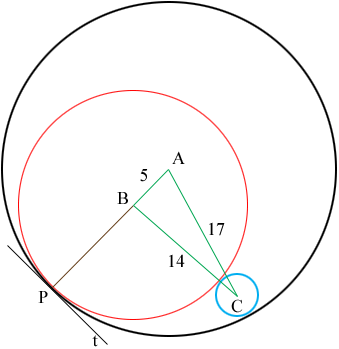
Suppose that the centres of the black, red and blue circles are $r_1, r_2 \mbox{ and } r_3$ respectively. From the diagram $r_2 + r_3 = 14.$

$P$ is the point of tangency of the black and red circles and $t$ is the tangent line to both circles at $P.$ the line segment $PB$ is then perpendicular to $t$ and likewise the line segment $AP$ is also perpendicular to $t.$ Hence $ABP$ is a line segment and hence $r_1 = 5 + r_2.$

Can you complete the solution from here?

Penny