Hi Heath,

I'm going to work in inches so the circumference of the tank is $57 \times 12 + 6 = 690$ inches. $690 / 8 = 86.25$ so I would start by marking 8 points on the circumference of the tank, 86.25 inches apart. The posts will be directly out from the tank at these positions.

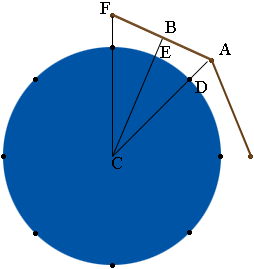
I have drawn the position of three of the posts and two of the eight fence sections. I want to look closely at the triangle $ABC$.

$CD$ and $CE$ are radii of the circular tank which has a circumference of 690 inches. The circumference of a circle is given by $2 \pi r$ where $r$ is the radius so

\[2 \pi r = 690\]

and hence

\[r = \frac{690}{2 \pi} = 109.8 \mbox{ inches.}\]

You told us that $|BE| = 36$ inches and hence $|BC| = 109.8 + 36 =145.8$ inches.

Angle $FCA$ measures $45$ degrees and hence angle $BCA$ measures $22.5$ degrees. Using some trigonometry $\cos(22.5) = \frac{|BC|}{|CA|}$ and hence

\[|CA| = \frac{|BC|}{cos(22.5)} = \frac{145.85}{0.9239} = 157.8 \mbox{ inches.}\]

$|CD| = 108.86$ inches so $|DA| = 157.8 - 108.86 = 49$ inches.

Go around the tank and measure out 49 inches from each of the 8 points you marked on the circumference of the tank. This should be the positions of the posts. There may be some error in the measurements so I would check the distance between the post positions before digging post holes. The distance between the posts, for example $|FA|$ should be consistent and you may need to do some fine tuning to guarantee this. My calculation give me that $|FA| = 120.8$ inches.

I hope this helps,
Harley