A player runs from second base to third base

HOME

Math Central

Quandaries & Queries

Question from Marie, a student:

A baseball diamond is a square with side 90 feet in length. A player runs from second base to third base at a rate of 18 ft/sec. At what rate is the area of the trapezoidal region, formed by line segments A, B, C, and D changing when D is 22.5
Distance A is the players distance from first base when running from 2nd to third. Distance D is his distance from 3rd base. Distance C is the distance from 3rd to 3rd to Home. Distance B is the distance from Home to First.
I have found dA/dt in a previous problem.

Hi Marie,

I drew what you described and used $P$ to label the player.

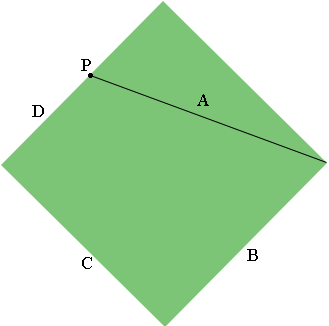
ball diamond

The area of the diamond is $90^2$ square feet and the area of the trapezoidal region formed by A, B, C and D is the area of the diamond minus the area of the triangle formed by first base, second base and the player. This is a right triangle with base length of $90$ feet and height $90 - D$ feet.

Write an expression for the area of the trapezoidal region and then differentiate it with respect to t. Evaluate this expression when $D = 22.5$ feet. Is the area increasing or decreasing when $D = 22.5$ feet?

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.