Hi Meredith,

Here is my diagram.

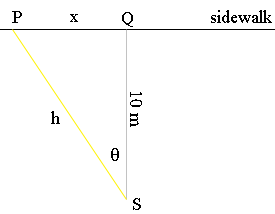
$S$ is the searchlight $P$ is the person and the triangle $QPS$ is a right triangle. $\theta$ is measured counterclockwise and hence if the person is walking towards $Q$ then $\large {\frac{d\theta}{dt}}$ and $\large{ \frac{dx}{dt}}$ are both negative where $t$ is time in seconds. You want $\large \frac{d\theta}{dt}$ when $h$ is 25 meters. Since you know $\large \frac{dx}{dt}$ I would look for a relationship between $x$ and $\theta.$ What I see is that$ \frac{x}{10} = \tan \theta$ so $x = 10 \tan \theta.$

Differentiate both sides of the above equation with respect to $t$ to obtain a relationship involving $\large \frac{dx}{dt}, \frac{d\theta}{dt},$ and $\theta.$ You will need to evaluate $\theta$ when $h$ is 25 meters.

Penny