Michael,

I drew a diagram of your hopper, upside down, and extended the edges to meet at P (orange lines in the diagram).

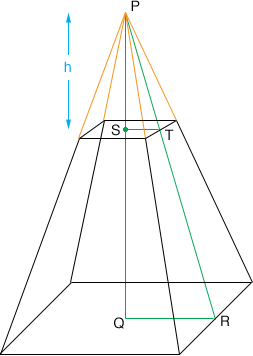
I extended the edges in this way because I can find the volume of a pyramid. The volume of your hopper is the volume of a pyramid with a 72" by 72" square base and height $PQ$ minus the volume of the pyramid with base 10" by 10" and height $PS,$ which I called $h$ in the diagram.

The volume of a pyramid is $\frac13 \times \mbox{ (the area of the base) } \times \mbox{ (the height)}.$ You can find the areas of the bases of both the pyramids I mentioned above and since you know that $QS$ is of length 31" all you need to complete the calculation is to find the height $h.$ For this I use the triangles $PQR$ and $PST.$ These triangles are similar and hence

\[\frac{|PQ|}{|QR|} = \frac{|PS|}{|ST|}.\]

$|QR| = \frac{72}{2} = 36$ inches, $|ST| = \frac{10}{2} = 5$ inches and $|SQ| = 31$ inches. Also $|PQ| = |PS| + |SQ| = h + 31$ and hence

\[\frac{h + 31}{36} = \frac{h}{5}.\]

Solving this for $h$ yields $h = 5$ inches.

Hence the volume of your hopper is

\[\frac13 \times (72 \times 72) \times (31 + 5) - \frac13 \times (10 \times 10) \times 5 \mbox{ cubic inches }.\]

For this I get 62,041 cubic inches.

To convert this to cubic feet ask Google. Type 62,041 cubic inches in cubic feet into the Google search window and Google will respond with 62 041 (cubic inches) = 35.9033565 cubic feet.

Penny