A line tangent to f(x)=1/x

HOME

Math Central

Quandaries & Queries

Question from Michael, a student:

A line tangent to f(x)=1/x in the first quadrant creates a right triangle with legs the x-axis and the y-axis. Prove that this triangle is always 2 square units regardless of where the point of tangency is.

Hi Michael,

First draw a diagram.

y=1/x

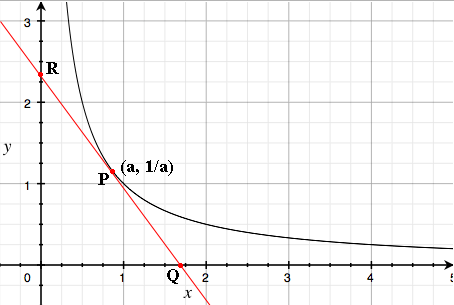
Let $P$ be a point on the graph with first coordinate $a$ then its second coordinate is $\large \frac{1}{a}.$ Find the slope of the tangent to $y = \large \frac{1}{x}$ at $P.$ I'm going to call this slope $m.$ Find the equation of the line through $P$ with slope $m.$ Find the coordinates of $Q$ and $R,$ the points where this line crosses the $x$ and $y$ coordinates. Find the area of the right triangle with vertices $Q, R$ and the origin.

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.