| |||
| Math Central | Quandaries & Queries |
|
Question from mike, a student: A water tank has the shape of a right circular cone with height 12 feet and radius 8 feet. Water is running into the tank so that the radius r (in feet) of the surface of the water is given by r=0.75t where t is the time (in minutes) that the water has been running. the volume V of the water is given by V=1/3 pi r^2h. Find V(t) and use it to determine the volume of the water when t=5 minutes. |
Hi Mike,
What you are missing is the height, h(t) of the water at time t minutes. Similar triangles helps determine this.
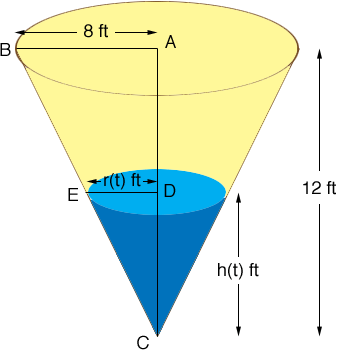
Triangles ABC and DEC are similar so
12/8 = h(t)/r(t).
You know that r(t) = 0.75 ft so substitute into this expression and solve for h(t). Now substitute r(t) and h(t) into the expression for the volume to determine Vt).
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.