| |||
| Math Central | Quandaries & Queries |
|
Question from MJ, a student: A rocket that is rising vertically is being tracked by a ground level camera located 3 mi from the point of blast off when the rocket is 2 mi high its speed is 400mph At what rate is the (acute) angle between the horizontal and the camera's line of sight changing |
Hi again MJ,
This problem is quite similar to the previous one you sent. In this problem I would draw a diagram.
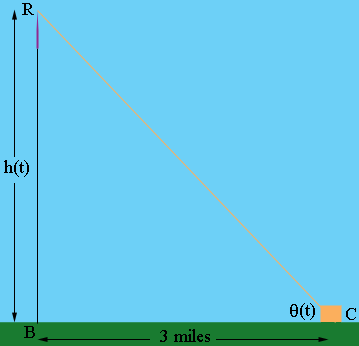
$R$ is the rocket at time $t,$ $B$ is the blastoff point and $C$ is the camera. $h(t)$ is the height of the rocket in miles at time $t.$ The angle between the horizontal and the line of sight of the camera I called $\theta(t).$
You are asked to find the rate of change of $\theta(t)$ at the time when $h(t) = 2$ miles and $h^\prime(t)$ is 400 miles per hour. To do this you need to find a relationship between $h(t)$ and $\theta(t).$ What trig function relates $h(t), \theta(t)$ and the side $BC$?
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.