| |||
| Math Central | Quandaries & Queries |
|
Question from MK, a student: Sam hits a golf ball with a five-iron a distance of 120m horizontally. A tree 45m high and 35m in front of Sam is directly in the path of the ball. Will the ball clear the tree if the ball makes a parabolic curve and has a maximum height or 80m? |
MK,
The problem we have to solve here is to see if the height of the tree, 45m, is larger or smaller then the value of the parabola at 35. That will determine of the golf ball will hit the tree or not.
We should begin this problem by drawing a picture and inserting in all of our known information. From the picture, we see that the tree is before the maximum height of the shot and is at the point (35, 45). The maximum height of the golf ball is at (60, 80) and the final position of the golf ball is at (120, 0).
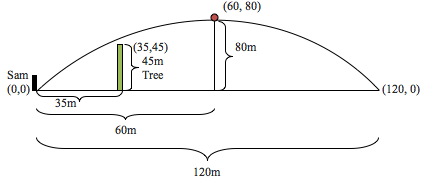
NOTE: From the picture I drew it looks like the tree is smaller than the golf ball trajectory, but I did this so we don’t assume the tree is a point on the parabola. Again the problem we have to solve is to see if the height of the tree, 45m, is larger or smaller then the value of the parabola at 35. So in reality the tree can be drawn 3 ways, below the parabola, above the parabola or right on the parabola.
In order to solve this problem we need to determine the equation for the parabola, which is golf ball’s trajectory, once we have that we need to see what the value of the parabola is when x = 35. If it is less than 45 then the golf ball will hit the tree, if it is more than 45 then the golf ball will clear the tree.
To create the equation for the parabola we will use one of the general forms of a parabola which is y = a(x - p)2 + q, where (p,q) is the coordinates of the parabola’s vertex, which we know is (60, 80). Plugging that in we get y = a(x - 60)2 + 80. From here we need to determine the value of a too obtain the equation for the parabola. To determine the a value that we need to use another point that is on the parabola (either the origin (0,0) or the final position of the golf ball). We can’t choose the position of the tree, because we don’t know if it is on the parabola or not. That is what we are trying to figure out. Choosing the origin we get 0 = a(x - 60)2 + 80, then we solve this equation for a getting a = -1/45, giving us the final equation y = (-1/45)(x - 60)2 + 80 for the parabola. From here we just have to insert the value of 35m into the equation for x and see if the y value is larger or smaller than 45.Hope this helps,
Brennan Yaremko
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.