Priyam,

I can give you some hints.

Here is my diagram

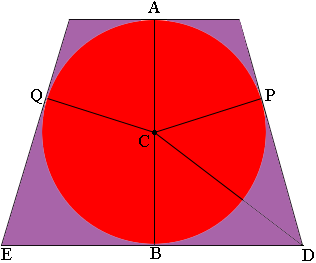
The sides of the trapezoid are tangent to the circle at $A, B, P \mbox{ and } Q.$ An important fact is that at each of these points the radius and tangent are perpendicular.

$ACB$ is a straight line. Do you see why? Since the trapezoid is isosceles the symmetry of the diagram tells us that $B$ is the midpoint os the side $DE$ and hence you know the length of $BD.$

Triangles $PCD$ and $CBD$ are congruent. Do you see why? Thus you know the length of $PD.$

Can you complete the problem now?

Write back if you need more help.

Penny