Tiling a swimming pool - Math Central

HOME

Math Central

Quandaries & Queries

Question from rustom, a student:

(a) Find the volume of water in swimming pool with vertical ends and sides
. The length measured at the water line is 50 ft. and the breadth is 20 ft. The
bottom of the swimming pool is a plane sloping gradually downward so that
the depth of the water at one end is 4 ft. and 8ft. at the other end.
(b) If the sides, ends, and bottom of the swimming pool are constructed of
tile blocks whose glaze surface dimensions are 3in by 6in. , and if the ends
and sides of the pool extend 2ft.above the water level, find the number of
blocks used if 1/20 of the surface area is covered by sealing material.

I got the (a) question but I don't know the (b) question which have the answer
of 16,136 blocks. I hope I can get the procedure for this, THANK YOU!

Hi Rustom,

I found the wording of part (b) confusing. I think that by "1/20 of the surface area is covered by sealing material" that 1/20 of the surface area is taken up by the grout between the tiles so that only 19/20 of the surface area is covered by the tiles.

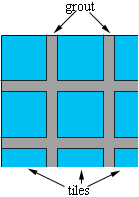
tiles

I found the surface area of the 5 pieces making sure that the heights of the sides were increased by 2 feet and using Pythagoras' Theorem to find the length of the bottom. I got 2139.19 square feet. The surface area covered by the tiles is then

$\frac{19}{20} \times 2123.19 = 2017.04$ square feet.

Each tile covers $\frac{3}{12} \times \frac{6}{12} = \frac{1}{8}$ square feet so it takes 8 tiles to cover 1 square foot. Hence you will need $8 \times 2017.04 = 16136.28$ tiles. You need to check all my arithmetic.

If this were an actual project you would need to round up. The tiles won't fit exactly and some will need to be cut producing some wastage.

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.