| |||
| Math Central | Quandaries & Queries |
|
Question from rustom, a student: Two vertical conical tanks (both inverted) have their vertices connected by a short horizontal pipe. I did not understand how the question works, whether the volume of the water from the |
Initially all the water is in the smaller tank.
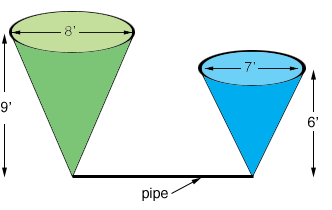
Once the water is allowed to flow through the pipe the atmospheric pressure forces the water to flow through the pipe until the system reaches an equilibrium state where the water in both tanks is the same height $h$.
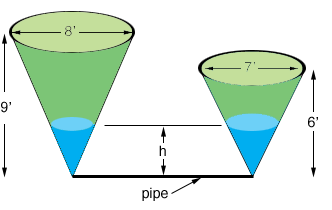
It is this height $h$ that you want.
Write back if you need more help,
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.