Ryan,

There are two things wrong with the statement of the problem, so it is not surprising that you are confused. So am I! The word "lateral" is not the right word -- it means "on the side" or "to the side", which is meaningless here. We can probably guess what is intended by the question, but first we should make sure we know what a parallelepiped is: it is a polyhedron with 6 faces (like a cube), but the opposite pairs of faces are congruent parallelograms. In your problem we are told that the bottom of your parallelepiped is a 4 by 6 rectangle, and therefore so is the top. We are told that another pair of faces, say front and back, are parallelograms with sides of length 8 and 6 that come together at a 45 degree angle. Unfortunately we are not told the shape of the remaining pair of faces (left and right). We must GUESS that it was intended for the front and back faces to be vertical, so that the remaining faces are 4 by 8 rectangles (slanted at a 45 degree angle to the base plane).

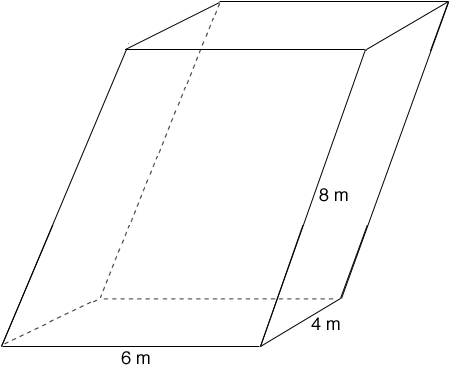
We can now find the volume, which is equal to the area of the base times the height:

AREA (base) = 4 X 6 = 24 square m.

I'll let you find the height -- which is the length of a leg of an isosceles right triangle whose hypotenuse is 8.

The volume is then 24*h cubic m. But remember we had to guess that the front and back faces are in vertical planes. Otherwise, there is insufficient information to determine the volume!

Chris