Hi Shelby,

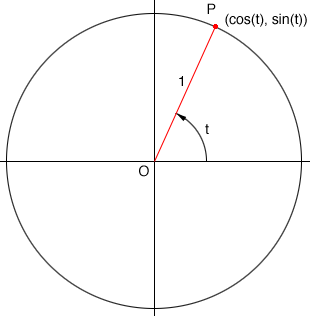
I find that the circle approach is the best way to approach this type of problem. Draw a circle with radius 1 unit and center at the origin $O.$ Draw a line segment from $O$ to a point $P$ on the circumference of the circle and measure the angle counterclockwise from the positive X-axis to the line segment $OP.$ If the measure of this angle is $t$ radians then $P$ has coordinates $\left(\cos(t), \sin(t)\right).$

You want the measure of the angle $t$ so that $\cos(t) = \frac{-1}{\sqrt 2}.$ Since $\cos(t)$ is the X-coordinate I drew the line $x = \frac{-1}{\sqrt2}$ to see where this line intersects the circle. There are two points $Q$ and $R$ in the diagram so there are two angles with measures $t_1$ and $t_2$ that have $\cos(t_1) = \cos(t_2) = \frac{-1}{\sqrt 2}.$

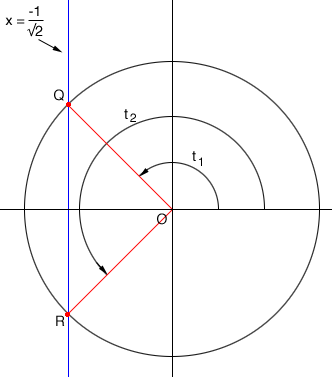
Let's look at $t_1$ more carefully.

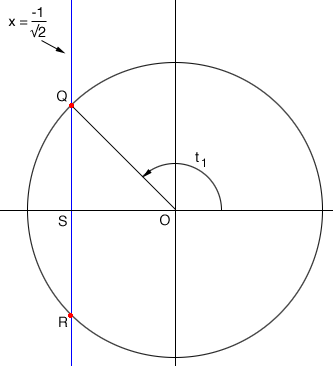
Triangle $QSO$ is a right triangle, the length of $OQ$ is 1 unit and the length of $SP$ is $\frac{1}{\sqrt2} \mbox{ units.}$ Use Pythagoras theorem to find the length of $QS.$ What does that tell you about the triangle $QOS?$ What is the measure of the angle $SOQ?$ What is the angle measure $t_1?$

Apply a similar approach to fine the angle measure $t_2.$

I hope this helps,
Penny