Hi Silvan,

The answer to your question relies on what is perhaps the best known result in all of mathematics called the Theorem of Pythagoras. The theorem states that

In any right triangle, the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angle).

Said algebraically the theorem is

If a right triangle has sides of length a, b and c where c is the length of the side opposite the right angle then a² + b² = c².

The converse is also true

If a triangle has sides of length a, b and c and a² + b² = c² then the triangle is a right triangle with the right angle opposite the side of length c.

Pythagoras lived from 570 to 495 BC but there is considerable evidence that this result was known much earlier.

Why does this have any connection to your question? Let me draw a picture of a circular clock face with centre at (0, 0) and with a point (x, y) on the circumference.

Next draw a vertical line segment from (x, y) to the x-axis and a line segment from (x, y) to (0, 0).

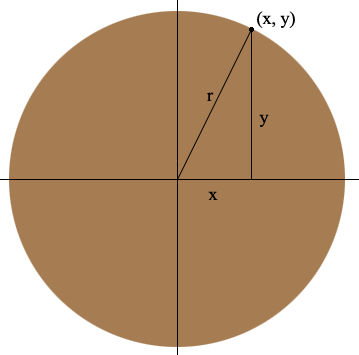
What I see now is a right triangle with sides of length x, y and r where r is the radius of the circle. Hence by the Theorem of Pythagoras, x² + y² = r². The converse of the Theorem of Pythagoras implies that if (x, y) is any point in the plane and x² + y² = r² then (x, y) must lie on the circumference of the circle with center (x, y) and radius r. This then gives you the answer to your question.

If (x, y) is a point in the plane then (x, y) lies on the circumference of the circle with center (0, 0) and radius r if and only if x² + y² = r².

Penny