Hi Steffi,

I think the second equation should be $x^2 +y^2 -4x -20y + 52=0.$

You should first complete the squares to express both equations in the form $(x - h)^2 + (y - k)^2 = r^2.$ This shows that the two equations are equations of circles. You will also find that in each case $h = 2$ and hence the two circles have their centres on the line $x = 2.$ Thus any circle that passes through the intersection points of these circles must also have its centre on the line $x = 2.$ Here is my diagram.

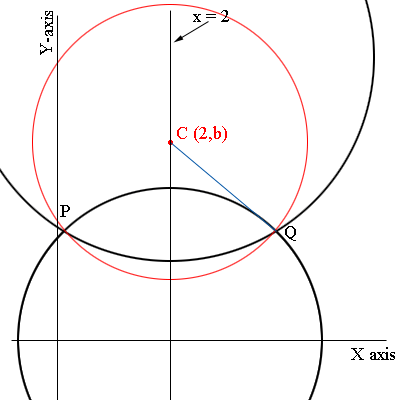
The two given circles are in black, $P$ and $Q$ are their points of intersection, $C$ is a point on the line $x = 2$ and the red circle has centre C and passes through $P$ and $Q.$ This circle then has equation $(x - 2)^2 + (y - b)^2 = r(b)^2$ where $r(b)$ is the distance from $C$ to $Q.$ I wrote the radius $r(b)$ since the distance from $C$ to $Q$ depends on $b.$

Solve the equations of the two black circles to find the coordinates of $P$ and $Q.% Find $r(b),$ the distance from $C$ to $Q$ and then $(x - 2)^2 + (y - b)^2 = r(b)^2$ is the family of circles you need.

I hope this helps,
Penny