| |||
| Math Central | Quandaries & Queries |
|
Question from terry, a parent: i have a 18 ft diameter gravel circle laid down for a fire pit. i want to lay the paver stones out in a octagon pattern. How long would the sides of my octagon be to fit center on the 18 ft diameter of gravel base? |
Hi Terry,
In my diagram the length of $CA$ is 9 feet and $D$ is the midpoint of $AB.$
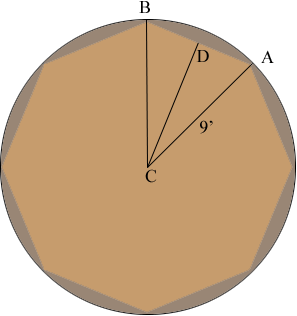
The measure of angle $BCA$ is $\frac{360^o}{8} = 45^o$ and hence the measure of angle $DCA$ is $22.5^o.$ If the side length $BA$ is $s$ feet then
\[\sin(DCA) = \sin(22.5^o) = \frac{|AD|}{|CA|} = \frac{s/2}{9}\]
and hence
\[\frac{s}{2} = 9 \times \sin(22.5^o) = 3.444 \mbox{ feet.}\]
Thus the side length $|AB|$ is $2 \times 3.444 = 6.888$ feet which is approximately $6$ feet $10$ and $\frac{11}{16}$ inches.
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.