Hi Tom,

I hope my diagram will help with this.

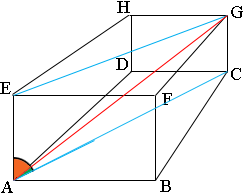
A diagonal is a line joining two vertices that does not lie on a face of the parallelepiped. I have indicated one of them $AG$ by a red line. I want to consider the angle between this diagonal and one of the faces, $ABCD$. The angle between a line and a plane is the smallest angle $GAP$ where $A$ is the point of intersection of the line and the plane, $G$ is another point on the line and $P$ is another point on the plane. The fact that $ABCDEFGH$ is a rectangular parallelepiped leads to the fact that the angle $GAC$ in the diagram is the angle you need. Again the rectangular nature of the diagram gives a way to find the measure of this angle.

You know the length of $CG$. You can calculate the length of $AC$. Do you see how? Now you can find the measure of the angle $GAC$. Do you see how?

Write back if you need more assistance,
Penny