Tom,

This question and also the question you sent earlier

a right circular cylinder is inscribed in a right circular cone of altitude h and radius of base x, as shown in the figure. Find the radius of the cylinder if its lateral area is equal to the lateral area of the small cone which surmounts the cylinder

both depend on finding an expression for the lateral surface area of a cone.

Suppose you have a cone with base radius $r,$ height $h$ and slant height $s$ as in the diagram.

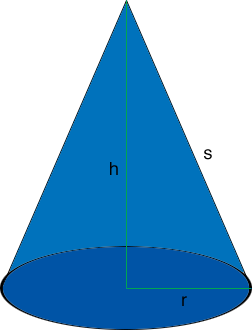
Notice that the triangle with sides $r, s \mbox{ and } h$ is a right triangle so if you know the lengths of two of the sides you can use Pythagoras' Theorem to find the length of the third side.

If you slit the side along the slant edge from the base to the apex the lateral surface of the cone will lie flat and form a sector of a circle. The radius of the circle is $s$, the length of the arc bounding the sector is the circumference of the circular base of the cone which is $2 \pi r,$ and the central angle has unknown measure $\theta$ radians.

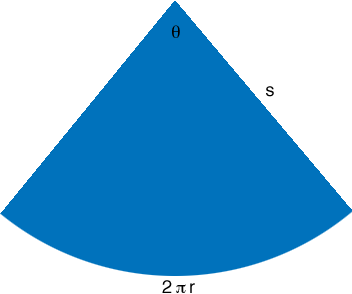
The lateral surface of the cone is this sector and the area of the sector is given by

\[\pi s^2 \theta.\]

The symmetry of a circle tells us that the ratio of the angle $\theta$ radians to the angle of the entire circle, $2 \pi$ radians is the same as the ratio of the length of the arc, $2 \pi r$ to the circumference of the circle of radius $s, 2 \pi s.$ That is

\[\frac{\theta}{2 \pi} = \frac{2 \pi r}{2 \pi s}.\]

and hence

\[\theta = 2 \pi \frac{r}{s}\]

Substituting this into the expression for the area of the sector and simplifying gives the area of the lateral surface of the cone as $r s \pi$ square units.

For the current problem imagine that the cone is sliced off at a height of $y$ units as in the diagram.

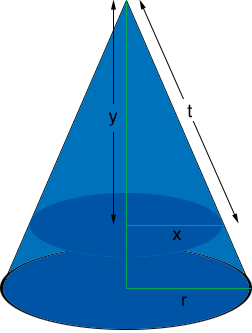
Use the expression above for the lateral surface area to give an expression for the surface area of the top part of the cone. If this area is half the surface area of the original cone this will give an equation relating $r, s, x \mbox{ and } t.$ Use the fact that the triangle with sides of length $r, s \mbox{ and } h$ in the first diagram is similar to the triangle with sides of length $x, t \mbox{ and } y$ in the third diagram to convert the equation relating $r, s, x \mbox{ and } t$ to one that gives $y$ in terms of $h.$

I hope this helps,
Penny