Hi Wayne,

The inverse sine function is usually defined or angles between $- \pi$ radians and $\pi$ radians. That's the way my calculator works and so if I ask for $\sin^{-1}(-0.25)$ my calculator returns $-0.2527$ radians, which is $0.2527$ radians measured clockwise from the positive x-axis. (Make sure you have your calculator set on radians not degrees.)

Let's look at a diagram.

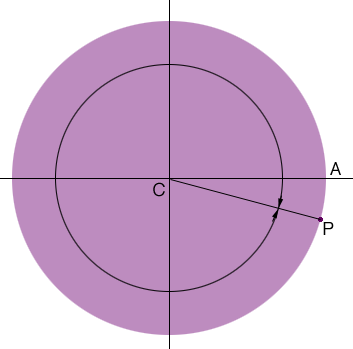
The circle has radius 1 unit and the point $P$ has y-coordinate $-0.25.$ My calculator then returned the radian measure of the angle $ACP$ measured clockwise. The answer you have is a positive value so it is the angle $ACP$ measured counterclockwise. The radian measure of this angle is $2 \pi - 0.2527 = 0.6030.$

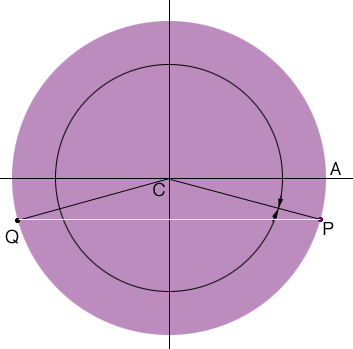
The second point on the unit circle is the point $Q$ above so the second value of $x$ so that $\sin x = -0.25$ is the angle $ACQ$ measured counterclockwise. What is its radian measure?

Penny