The best way to approach this is to center the circle on the origin of a normal graph and use x as your independent variable.

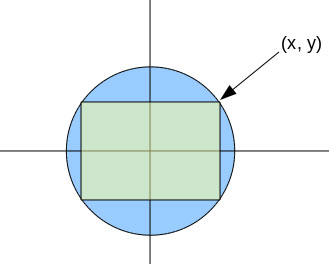
Now it should be clear to you that the perimeter is simply 4(x+y). Thus, we really only need to think about the first quadrant.

x varies from 0 to R, of course, and so does y. But you can express f(x) = y by re-arranging the circle's equation

R² = x² + y².

Then just find the minimum and maximum values of the expression x + f(x) and multiply by four.

Cheers,
Stephen La Rocque.