A square surrounded by dots

HOME

Math Central

Quandaries & Queries

Question from A, a parent:

Okay so my daughter came home and had this question for homework from her teacher. I have no idea what it means HELP!!
The question shows a figure that is a square. It has 5 dots on the top, bottom and on the sides looks similar to this:
. . . . .
.        .
.        .
.        .
. . . . .
they want to know 3 more ways to show the number of dots in the figure. They have already shown one with just counting them
and the other one that they showed was circling the four corner dots and then taking the dots in between with a number sentence set up
like this: 4+4*(5-2) = 4+4*3= 16. They also besides giving 3 ways want us to write a number sentence and an algebraic sentence to show the number of
dots in the figure with "n" sides. Please help! So confusing ! I don't know if my square turned out or not but it should be 5 across the top and bottom and
on the sides and no dots in the middle it is just the outside.

Hi,

Here is my display of dots.

dots

What if you circle three dots in each corner.

dots

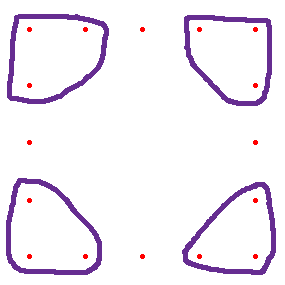
There are 3 dots in each circle and you have removed 4 dots from each side so you have the number sentence $4 \times 3 + 4\times(5 - 4).$

What if you walk around the square in a counterclockwise direction starting at the upper right corner. Every time you get to a corner you circle the corner dot and the next dot after it.

dots

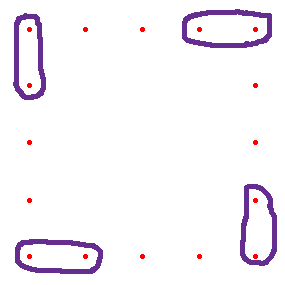
You have 4 groups of 2 dots that are circled and 4 groups of (5 - 3) dots that are not circled. Thus you have $4 \times 2 + 4 \times 2$ dots.

What about an n by n square? For the example given with the corner dot being circled you now have 4 dots circled and on each side all but 2 are not circled. Thus you have $4 + 4 \times (n - 2)$ dots.

See if you can mimic the two techniques I used but with an n by n square.

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.