| |||
| Math Central | Quandaries & Queries |
|
question from Alysia, a student: I'm having trouble with this question and was wondering if someone could help me work this problem out. The scores on a test taken by 1000 students are normally distributed with a mean of 66 and standard of deviation of 12. If the college wishes only the top 8% of people to get an A, what would the cutoff score be for the A's? |
Hi Alysia,
You first need to convert the normal distribution with random variable $X$ with mean $\mu = 66$ and standard distribution $\sigma = 12$ to the standard normal distribution with random variable $Z.$ The conversion is
\[Z = \frac{X - \mu}{\sigma} = \frac{X - 66}{12} \]
Now you need to use the standard distribution table to find the number $Z_{0.08}$ so that the area under the normal curve and to the right of $Z_{0.08}$ is $0.08,$ as illustrated in the diagram below.
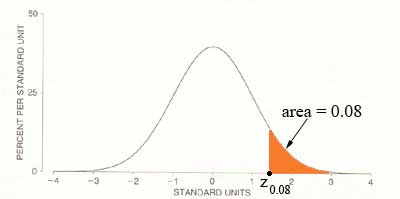
Set $Z = Z_{0.08}$ and solve for $X.$
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.