| |||
| Math Central | Quandaries & Queries |
|
Question from Carlos: I have a lot with a slope. On the right I need to bring it up 2', From that point to the left is 112' which at this point I need to bring it up 5' for it to be level . The distance front to back is 80'. What is the cubic yards of this area that I need to fill in. |
Hi Carlos,
I drew a rough sketch, not to scale
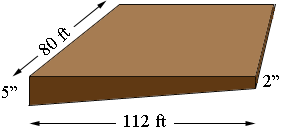
The volume of fill is the area of the cross section times the length of 80 fet. The cross section is a trapezoid and the area of a trapezoid is the average of the lengths of the parallel sides times the distance between the parallel sides. I want all the dimensions in feet so the parallel sides are of length $\large \frac{5}{12}$ feet and $\large \frac{2}{12}.$ Hence the volume of fill required is
\[\frac12 \left( \frac{5}{12} + \frac{2}{12} \right) \times 112 \times 80 \mbox{ cubic feet.}\]
There are 27 cubic feet in a cubic yard so divide the volume in cubic feet by 27 to obtain the volume in cubic yards.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.