Hi Crisfe,

I am not sure that I understand but I think you are asked to find the point P where the common chord intersects the line joining the centers.

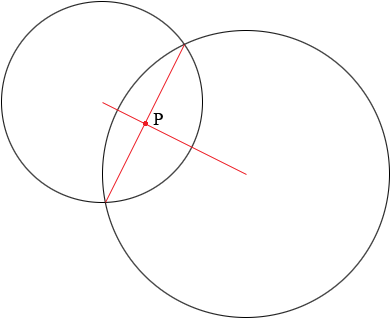
The point P is at the midpoint of the chord. Can you see why?

I can see two ways to approach this. One is algebraic. Substitute $x^2 + y^2 = 25$ into the second equation to give you a linear equation. Solve this equation for $y$ and substitute into $x^2 + y^2 = 25.$ Solve for $x$ and then $y$ and verify that you have the points of intersection of the circles.

The second method is essentially geometric. Complete the squares in the second circle $x^2 +y^2-12x-6y+35=0$ to put the equation in standard form so you can easily determine its center and radius. As accurately as you can draw the two circles. From the diagram guess at the points of intersection and then verify that you are correct.

Once you have found the endpoints of the chord you can find the midpoint of the chord.

I hope this helps,

Penny