Hi Fleur,

Here is my diagram of your lamp shade. I extended the sides to meet at P and added some labels.

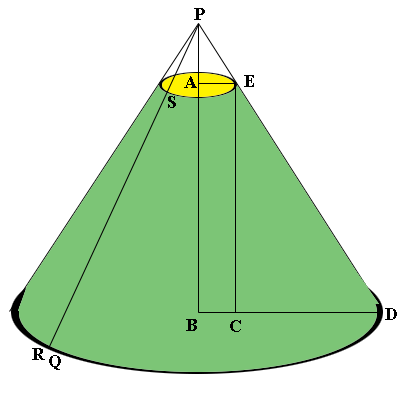
From your dimensions $|AE| = 4$ cm, $|BD| = 20$ cm, and $|AB| = 21$ cm. Triangles $BDP$ and $CDE$ are similar so

\[\frac{|PB|}{20} = \frac{21}{20 - 4}\]

so

\[|PB| = \frac{21}{16} \times 20 = 26.25 \mbox{ cm.}\]

Triangle ECD is a right triangle so Pythagoras Theorem says that

\[|SR| = |ED| = \sqrt{21^2 + 16^2} = 26.4 \mbox{ cm.}\]

Likewise triangle PBD is a right triangle and another use of Pythagoras Theorem shows that $|PR| = |PD| = 33$ cm.

Now slice the diagram from P to Q and roll it out to see the diagram below.

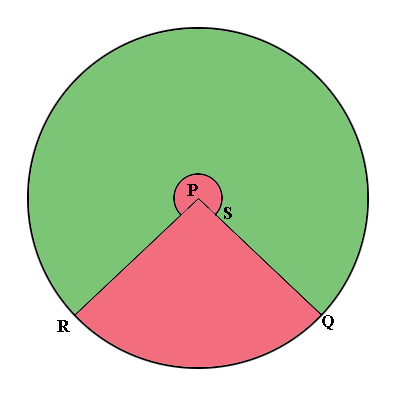
The external circle has radius 33 cm and the interior circle has radius 26.4 cm. The pink part is missing and it is the angle QPR you need to determine to complete the construction.

The circumference of the outside circle is $2 \pi \times 33$ cm and the counterclockwise arc from Q to R is the circumference of the base of the shade so its length is $2 \pi \times 20$ cm. The angle QPR is a fraction of the $360^o$ that makes up the circle. That fraction is

\[\frac{2 \pi \times 33 - 2 \pi \times 20}{2 \pi \times 33}= \frac{13}{33}\]

and $\large \frac{13}{33} \normalsize \times 360^o = 142^o.$

The construction is then to draw two circles with radii $33$ cm and $33 - 26.25 = 6.75$ cm, each with the same center P. Cut out the wedge QPR with center angle measure of $142^o$ and cut out the interior of the smaller circle. Roll up the remaining piece to form the lamp shade.

I suggest you try it with scrap paper first,
Penny