Hi Jan,

I drew a diagram of your dugout, not to scale.

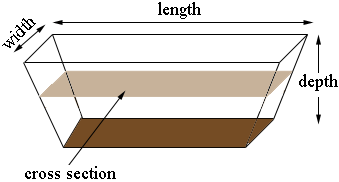
This shape is called a prismoid and the volume $V$ of a prismoid is given by

\[V = \frac{d}{6} \left( A_t + 4 A_m + A_b\right)\]

where $d$ is the depth, $A_t$ is the area of the top, $A_b$ is the area of the bottom and $A_m$ is the area of the cross section half way between the top and bottom.

In the example you sent $d = 12$ feet and $A_t = 120 \times 40 = 4800$ square feet. You have a slope of three to one so for every 3 feet you go down you lose 1 foot in length at each end and 1 foot in width at each side. Thus the bottom is $120 - 8 = 112$ feet by $40 - 8 = 32$ feet. Likewise the cross section, half way down is $116$ feet by $36$ feet. Thus the volume of the dugout in cubic feet is

\[V = \frac{12}{6} \left(4800 + 4 \times 116 \times 36 + 112 \times 32\right).\]

I got a result of $50,176$ cubic feet.

A cubic yard is $27$ cubic feet so the volume is $\large \frac{50,176}{27} = 1,858.4$ cubic yards.

I hope this helps,
Penny