| |||
| Math Central | Quandaries & Queries |
|
Question from Jean, a student: "A conical buoy that weighs B pounds floats upright in water with its vertex "a" feet below the surface. A crane on a dock lifts the buoy until its vertex just clears the surface. How much work is done?" Thanks, When the crane has lifted the buoy x feet, the force required to hold it in this position is the weight of the buoy minus the upward buoyant force F due to the water still displaced, and I don't know how |
Hi Jean,
Wikipedia Has a concise statement of Archimedes' principle
Any object, wholly or partially immersed in a fluid, is buoyed up by a force equal to the weight of the fluid displaced by the object.
— Archimedes of Syracuse
The volume of a cone is given by
volume = $\frac13 \pi \times $ radius2 $\times$ height.
Thus from my diagram
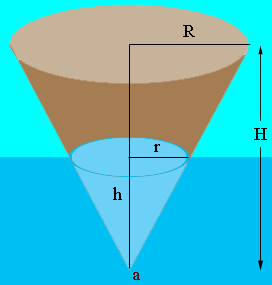
the weight of the buoy is
\[W_B = \frac13 \pi \times R^2 \times H \times\mbox{ (the density of the buoy material.)} \]
The buoyant force is equal to the weight of the fluid displaced by the buoy and this weight is given by
\[W_F = \frac13 \pi \times r^2 \times h \times\mbox{ (the density of water.)} \]
Thus, at any instance the force required by the crane is $W_B - W_F.$
Does this help? Write back if you need more assistance.
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.