Hi John,

I used the "washer" method and here is my diagram.

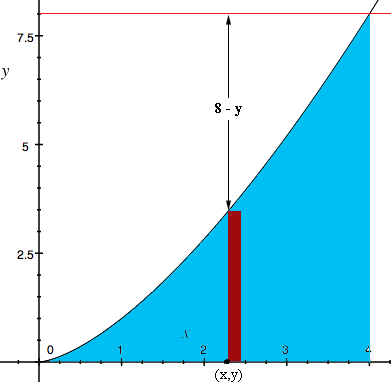
The dark red strip of width $\Delta x$ is rotated around the line $y = 8$ to produce the washer. The outer radius is then 8 units and the radius of the hole is $8 - y$ units. The volume of the washer is

\[\pi \; [8^2 - (8-y)^2] \Delta x = \pi \; [16 y - y^2] \Delta x\]

Use the fact that $y^2 = x^3,$ convert to an integral and solve.

Write back if you need more assistance.

Penny

John wrote back

Dear Penny: Thank you for your help. Here is my solution but its a long way from the book's answer of 704 pi divided by 5.
delta V=pi(R2^2-R1^2)delta x
= pi(8^2-(8-y)^2 )delta x
=pi ( 64-(64-16y + y^2)delta x )
V=the untegral from 0 to 2 (pi) (16x^(3/2)- x^(3/2)^2 dx
(if y^2=x^3 then y=x^(3/2))
my answer of:
V= pi[32x^(5/2)] - pi[x^3/3} doesn't look too good. I used
this integral once or twice before but my algebra is almost
as bad as my calculus. My answer is27.6 Please point out
which of the above steps is in error.

Thank you, very, very much
(grandpa John)

Hi again John,

The region to be revolved runs from $x = 0$ to $x = 4,$ so I don't know why you have the integral from 0 to 2. I get

\[V = \pi \int_{0}^{4} [16 x^{3/2} - x^3] dx.\]

An antiderivative of $x^{3/2}$ is $\large \frac25 x^{5/2}$ and an antiderivative of $x^3$ is $\large \frac14 x^4$ and hence I get

\[\pi \int [16 x^{3/2} - x^3] dx = \pi [16 \times \frac52 x^{5/2} - \frac14 x^4] .\]

Evaluating from 0 to 4 gives $V = \large \frac{407 \pi}{3}.$

Penny