we have two responses for you

Katherine,

You have an error, first move the constant across and get 8 cos^2 theta = 4

I think you know how to do the rest. Ideally, in this case, you should recognize the square root -without evaluating!- as the cosine of something familiar and be able to find the arccos without picking up a calculator. (Everybody who works with trig should know and recognize all six trig functions of 0, pi/6 [30 degrees], pi/4 [45 degrees], pi/3 [60 degrees], and pi/2 [90 degrees].)

Sketching a cosine curve should help you locate the other three values in the interval [0, 2 pi).

Note that you can add/subtract 2 n pi to/from any of these four values and get infinitely many other solutions outside the "principle period". Some instructors expect this, and there are situations where it's actually important.

Good hunting!
RD

Hi Katherine,

You are to solve for $\theta$ if $8 \cos(\theta) - 3 = 1.$ You should first add 3 to each side to get $8 \cos(\theta) = 4$ and then divide by 8 and take the square root to get

\[\cos(\theta) = \frac{\pm 1}{\sqrt 2}.\]

You should know that $\cos(45^o) = \frac{1}{\sqrt 2}$ so 45 degrees is one solution but how do you find all $\theta$ between 0 and 360 degrees that satisfy the equation? I would use the unit circle with centre at the origin $O.$

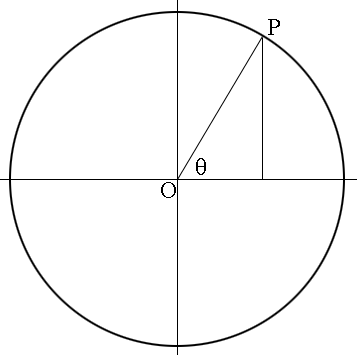
If you draw a ray from $O$ at an angle $\theta$ to the positive X-axis, measured counterclockwise, and it intersects the circle at $P,$ then the X-coordinate of $P$ is $\cos(\theta)$ and the Y-coordinate of $P$ is $\sin( \theta).$ (I drew a vertical line from $P$ to the X-axis so that you can use the triangle to see this if you are accustomed to using a right triangle to define the trig functions. Remember that the length of $OP$ is 1.)

What other point on the unit circle has the same X-coordinate?

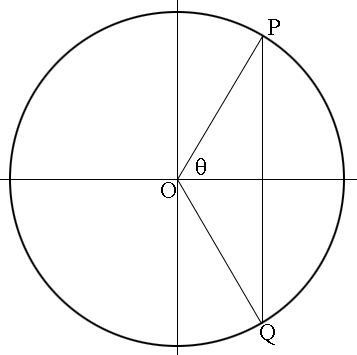
Extend the vertical line from P to intersect the circle at $Q.$ $Q$ has the same x-coordinate as $P$ and using symmetry the measure of the angle from the positive X-coordinate, clockwise to $OQ$ is $360 - \theta$ degrees. Hence $\cos(360 - \theta) = \cos(\theta).$

Try this technique with your problem, first starting with $\cos(\theta) = \frac{1}{\sqrt 2}$ and then with $\cos(\theta) = \frac{-1}{\sqrt 2}.$

Write back if you need more assistance,
Penny