The height of an isosceles triangle

HOME

Math Central

Quandaries & Queries

Question from ken:

I am trying to determine the various heights of an isosceles triangle, if each has the same base dimension and varies in the degree of the base (equal) angles. What is the method to do this?
As an example, of the base is 10, and the two equal angles are each 45 degrees, what is the height? With the same base (10), but with the two equal angles at 60 degrees, what is the height? And with the same base (10) and the two equal angles at 75 degrees, what would be the height?
I know how to calculate the degrees of the third angle (add the degrees of the known angles, and subtract from 180); but am unsure if that is needed for figuring the overall height.
And to be clear; I am not looking for the length of the sides of the triangle, but the height from the base to the top point.
Thank you!

Ken,

Wonderful question! You have made some very important observations. Your question shows impressive insight; what you have done is to discover for yourself the idea behind trigonometry. Fortunately, others have done all the hard work, so that the answer to your question comes down to using a calculator (or computer, if you prefer). The relationship you seek is called the TANGENT of the angle. It turns out to be more convenient to use HALF the base of your isosceles triangle.

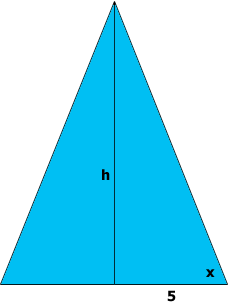
triangle

Half of your isosceles triangle is a RIGHT TRIANGLE whose height h equals the height of your isosceles triangle, and whose base equals 5. The tangent of the base angle -- call it x and measure it in degrees -- is then h/5, so that

\[h = 5\times \tan x.\]

For example,
for x = 45 degrees, $h = 5 \times \tan(45) = 5 \times 1 = 5;$
for x = 75 degrees, $h = 5 \times \tan(75)$ which is approximately $5 \times 3.73 = 18.65.$

Chris

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.