Hi Kodie,

The answer depends on what you are given.

If you are given two points in the plane and you want the slope of the line containing these two points then the slope is the rise over the run.

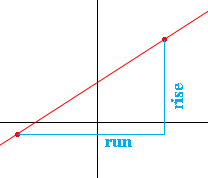
If you are given the coordinates of the points, $(x_1, y_1) \mbox{ and } (x_2, y_2)$ then the slope $m$ is given by

\[m = \frac{y_2 - y_1}{x_2 - x_1}\]

When I see the coordinates of two points I don't think of this formula . I think "the difference between the y coordinates divided by the difference between the x coordinates". You just have to make sure you take the differences in the same direction.

If you are given the equation of a line, for example $3x = 4y - 6,$ and you are to find its slope you need to put the line into the form $y = mx + b.$ For example my line above is $4y = 3x + 6$ or dividing by 4, $ y = \large \frac34 x+\frac64$ so the slope is $\large \frac34.$

Your question reminded me of a road sign I saw a couple of weeks ago while I was driving downhill

The sign indicated that the slope was 7% downhill or $m = -0.07.$

I hope this helps,
Penny